- Cálculo de los vectores propios
Una vez que se conocen los valores propios λ, los vectores propios se pueden hallar resolviendo el sistema de ecuaciones homogéneo:
Una forma más sencilla de obtener vectores propios sin resolver un sistema de ecuaciones lineales se basa en el teorema de Cayley-Hamilton que establece que cada matriz cuadrada satisface su propio polinomio característico. Así, si  son los valores propios de A se cumple que
son los valores propios de A se cumple que
 son los valores propios de A se cumple que
son los valores propios de A se cumple que
por lo que los vectores columna de  son vectores propios de
son vectores propios de 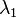 .
.
 son vectores propios de
son vectores propios de 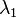 .
.
Sea A ∈ Mn y λ ∈ R.
El subespacio propio de A asociado a λ es el conjunto
Vλ formado por todos los vectores x ∈ R
n
tal que
(A − λIn)x =
−→0 .
Vλ es un subespacio vectorial de R
n
.
La multiplicidad geom´etrica de λ es la dimensi´on de Vλ.
 RSS Feed
RSS Feed Twitter
Twitter

0 comentarios:
Publicar un comentario