Ecuación del valor propio o autovalor
Matemáticamente, vλ es un vector propio y λ el valor propio correspondiente de una transformación T si verifica la ecuación:
donde T(vλ) es el vector obtenido al aplicar la transformación T a vλ.
Supóngase que T es una transformación lineal (lo que significa que  para todos los escalares a, b, y los vectores v, w). Considérese una base en ese espacio vectorial. Entonces, T y vλpueden representarse en relación a esa base mediante una matriz AT y un vector columna vλ—un vector vertical unidimensional. La ecuación de valor propio en esta representación matricial se representa de la siguiente forma:
para todos los escalares a, b, y los vectores v, w). Considérese una base en ese espacio vectorial. Entonces, T y vλpueden representarse en relación a esa base mediante una matriz AT y un vector columna vλ—un vector vertical unidimensional. La ecuación de valor propio en esta representación matricial se representa de la siguiente forma:
 para todos los escalares a, b, y los vectores v, w). Considérese una base en ese espacio vectorial. Entonces, T y vλpueden representarse en relación a esa base mediante una matriz AT y un vector columna vλ—un vector vertical unidimensional. La ecuación de valor propio en esta representación matricial se representa de la siguiente forma:
para todos los escalares a, b, y los vectores v, w). Considérese una base en ese espacio vectorial. Entonces, T y vλpueden representarse en relación a esa base mediante una matriz AT y un vector columna vλ—un vector vertical unidimensional. La ecuación de valor propio en esta representación matricial se representa de la siguiente forma:
donde la yuxtaposición es un producto de matrices. Dado que en esta circunstancia la transformación T y su representación matricial AT son equivalentes, a menudo podemos emplear sólo T para la representación matricial y la transformación. Esto es equivalente a un conjunto de n combinaciones lineales, donde n es el número de vectores de la base. En esta ecuación, tanto el autovalor λ y las n componentes de vλ son desconocidos. Sin embargo, a veces es poco natural o incluso imposible escribir la ecuación de autovector en forma matricial. Esto ocurre, por ejemplo, cuando el espacio vectorial es de dimensión infinita, como por ejemplo en el caso de la cuerda mostrada anteriormente. Dependiendo de la naturaleza de la transformación Ty el espacio al que se aplica, puede ser ventajoso representar la ecuación de autovalor como un conjunto deecuaciones diferenciales, donde los autovectores reciben a menudo el nombre de autofunciones del operador diferencial que representa a T. Por ejemplo, la derivación misma es una transformación lineal, ya que (si f(t) yg(t) son funciones derivables y a y b son constantes)
Considérese la diferenciación con respecto a  . Sus autofunciones h(t) obedecen a la ecuación de autovalor:
. Sus autofunciones h(t) obedecen a la ecuación de autovalor:
 . Sus autofunciones h(t) obedecen a la ecuación de autovalor:
. Sus autofunciones h(t) obedecen a la ecuación de autovalor: ,
,
donde λ es el autovalor asociado con la función. Una función en el tiempo es constante si 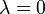 , crece proporcionalmente a sí misma si
, crece proporcionalmente a sí misma si  es positiva, y decrece proporcionalmente a sí misma si
es positiva, y decrece proporcionalmente a sí misma si  es negativa. Por ejemplo, una población ideal de conejos engendra con más frecuencia a medida que hay más conejos, y por tanto satisface la ecuación para lambda positivo.
es negativa. Por ejemplo, una población ideal de conejos engendra con más frecuencia a medida que hay más conejos, y por tanto satisface la ecuación para lambda positivo.
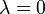 , crece proporcionalmente a sí misma si
, crece proporcionalmente a sí misma si  es positiva, y decrece proporcionalmente a sí misma si
es positiva, y decrece proporcionalmente a sí misma si  es negativa. Por ejemplo, una población ideal de conejos engendra con más frecuencia a medida que hay más conejos, y por tanto satisface la ecuación para lambda positivo.
es negativa. Por ejemplo, una población ideal de conejos engendra con más frecuencia a medida que hay más conejos, y por tanto satisface la ecuación para lambda positivo.
La solución a la ecuación de valor propio es  , la función exponencial; pues esa función es una función propia del operador diferencial d/dt con el valor propio λ. Si λ es negativa, la evolución de g se denomina decaimiento exponencial; si es positiva se denomina crecimiento exponencial. El valor de λ puede ser cualquier número complejo. El espectro de d/dt es entonces el plano complejo en su totalidad. En este ejemplo el espacio vectorial en el que actúa d/dt es el espacio de las funciones derivables de una variable. Este espacio tiene una dimensión infinita (pues no es posible expresar cada función diferenciable comocombinación lineal de un número finito de funciones base). No obstante, el espacio propio asociado a un valor propio determinado λ es unidimensional. Es el conjunto de todas las funciones
, la función exponencial; pues esa función es una función propia del operador diferencial d/dt con el valor propio λ. Si λ es negativa, la evolución de g se denomina decaimiento exponencial; si es positiva se denomina crecimiento exponencial. El valor de λ puede ser cualquier número complejo. El espectro de d/dt es entonces el plano complejo en su totalidad. En este ejemplo el espacio vectorial en el que actúa d/dt es el espacio de las funciones derivables de una variable. Este espacio tiene una dimensión infinita (pues no es posible expresar cada función diferenciable comocombinación lineal de un número finito de funciones base). No obstante, el espacio propio asociado a un valor propio determinado λ es unidimensional. Es el conjunto de todas las funciones  , donde A es una constante arbitraria, la población inicial en t=0.
, donde A es una constante arbitraria, la población inicial en t=0.
 , la función exponencial; pues esa función es una función propia del operador diferencial d/dt con el valor propio λ. Si λ es negativa, la evolución de g se denomina decaimiento exponencial; si es positiva se denomina crecimiento exponencial. El valor de λ puede ser cualquier número complejo. El espectro de d/dt es entonces el plano complejo en su totalidad. En este ejemplo el espacio vectorial en el que actúa d/dt es el espacio de las funciones derivables de una variable. Este espacio tiene una dimensión infinita (pues no es posible expresar cada función diferenciable comocombinación lineal de un número finito de funciones base). No obstante, el espacio propio asociado a un valor propio determinado λ es unidimensional. Es el conjunto de todas las funciones
, la función exponencial; pues esa función es una función propia del operador diferencial d/dt con el valor propio λ. Si λ es negativa, la evolución de g se denomina decaimiento exponencial; si es positiva se denomina crecimiento exponencial. El valor de λ puede ser cualquier número complejo. El espectro de d/dt es entonces el plano complejo en su totalidad. En este ejemplo el espacio vectorial en el que actúa d/dt es el espacio de las funciones derivables de una variable. Este espacio tiene una dimensión infinita (pues no es posible expresar cada función diferenciable comocombinación lineal de un número finito de funciones base). No obstante, el espacio propio asociado a un valor propio determinado λ es unidimensional. Es el conjunto de todas las funciones  , donde A es una constante arbitraria, la población inicial en t=0.
, donde A es una constante arbitraria, la población inicial en t=0. RSS Feed
RSS Feed Twitter
Twitter


0 comentarios:
Publicar un comentario