Vectores y Valores Propios ~ Vector y Valores Propios

Vectores y Valores Propios

Formalmente, se definen los vectores propios y valores propios de la siguiente manera: Si A: V → V es un operador lineal en un cierto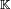

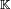\scriptstyle \mathbb{K}

espacio vectorial V, v≠0 es un vector diferente de cero en V y c es un escalar tales que

$\mathbf{A} \mathbf{v} = c \mathbf{v},\qquad \mathbf{v}\ne \mathbf{0}, c \in \mathbb{K},$

entonces decimos que v es un vector propio del operador A, y su valor propio asociado es c. Observe que si ves un vector propio con el valor propio c entonces cualquier múltiplo diferente de cero de v es también un vector propio con el valor propio c. De hecho, todos los vectores propios con el valor propio asociado c junto con 0, forman un subespacio de V, el espacio propio para el valor propio c. Observe además que un espacio propio Z es un subespacio invariante de A, es decir dado w un vector en Z, el vector Aw también pertenece a Z.