Teoremas de descomposición para matrices generales ~ Vector y Valores Propios

Teoremas de descomposición para matrices generales

El teorema de descomposición es una versión del teorema espectral en una clase concreta de matrices. Este teorema se explica normalmente en términos de transformación coordinada. Si U es una matriz invertible, puede verse como una transformación entre un sistema de coordenadas a otro, donde las columnas de U son las componentes de la nueva base de vectores expresados en términos de la base anterior. En este nuevo sistema las coordenadas del vector

v

se representan por

v'

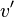, que puede obtenerse mediante la relación

v'=Uv

y, por otra parte, se tiene

v=U^{-1}v'

. Aplicando sucesivamente

v'=Uv

,

w'=Uw

y

U^{-1}U=I

, a la relación

Av=w

proporciona

A'v'=w'

con

A'=UAU^{-1}

, la representación de A en la nueva base. En esta situación, se dice que las matrices A y

A'

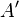son semejantes.

El teorema de descomposición declara que, si se eligen como columnas de

U^{-1}

n vectores propios linealmente independientes de A, la nueva matriz

A'=UAU^{-1}

es diagonal y sus elementos en la diagonal son los valores propios de A. Si esto es posible, entonces A es una matriz diagonalizable. Un ejemplo de una matriz no diagonalizable es la matriz A ya mostrada:

A=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}.

Hay muchas generalizaciones de esta descomposición que pueden tratar con el caso no diagonalizable, diseñadas con diferentes propósitos:

la descomposición de Schur declara que toda matriz es equivalente a una matriz triangular.
la descomposición en valores singulares, $A=U \Sigma V^*$ donde $\Sigma$ es diagonal con U y V matrices unitarias, los elementos de la diagonal de $A=U \Sigma V^*$ no son negativos y reciben el nombre de valores singulares de A. Esta descomposición también puede hacerse en matrices no cuadradas.
la forma normal de Jordan, donde $A=X \Lambda X^{-1}$ y $\Lambda$ no es diagonal sino diagonal por bloques. El número y tamaño de los bloques de Jordan están determinados por las multiplicidades geométrica y algebraica de los valores propios. La descomposición de Jordan es un resultado fundamental. A partir de ella se puede deducir inmediatamente que una matriz cuadrada está descrita completamente por sus valores propios, incluyendo la multiplicidad. Esto muestra matemáticamente el importante papel que desempeñan los valores propios en el estudio de matrices.
como consecuencia inmediata de la descomposición de Jordan, cualquier matriz A puede escribirse de forma única como A=S + N donde S es diagonalizable, N es nilpotente (por ejemplo, tal que N^q=0 para un cierto q), y S cumple la propiedad conmutativa del producto (SN=NS).